StʌrunneR

1984

　　有一天，我的父亲给我讲故事，他说，1984年。
　　1984年我的一个很远很远很远很远的远房亲戚参加了高考，那是一届传奇的高考。据说那一届高考数学没有一个人拿了满分。
　　“或许是有的。”父亲说。
　　
　　有一天，欧洲的三个数学家突然打了一个寒战。数列，他们说，数列数列数列。于是他们互相打电话，他们在电话里说：“数列。”另一头说：“数列数列。”于是他们决定合作出版一本书叫《数列》。
　　“你有没有看过一本叫《数列》的书？”
　　“看过看过，写的太好了。”我说，父亲糊涂了，狗都认识数列的封面。
　　三个数学家于是开始埋头苦干。他们每天互相打电话确认情况。他们说12345678，数到几表示写到哪里。但是有一天，他们在电话里都不说话了。
　　“汪，”他们说，“汪。”
　　于是他们像狗一样的到处飞来飞去找世界上各个地方的数学家求助。
　　
　　（如果你想知道为什么，我无法让一个普通的人明白。这篇文章写出来已经犯了禁忌了，我想我或许可以冒险再说一下他们在本子上写了什么。
　　(F************)
　　
　　但是就像传统武侠小说那样，江湖上的人没有一个解得了此毒。于是一时刀光剑影，邪气逆流，平静江湖突然卷入危急存亡之秋。
　　事实上最初的喧闹过后，人们就逐渐淡忘了这件事情。没有人会在乎三个数学家，因为数学家的发明除了难为其他人之外不会有任何用处。更重要的是，人们发现他们嘴里叽里呱啦的声音没一个人听得懂。
　　“数列。”他们说。
　　
　　后来他们三个人就上了山，因为山上住着的东西绝对不寻常。他们想如果山上是一条龙，那么或许被吃掉可以关上他们不受控制的嘴；如果山上是一个仙人，或许仙人可以给他们指点与答案。但令人失望的是，不像大多数武侠小说，他们上了山以后就发现了一个球。
　　
　　球说：“如果你们想……”
　　他们说：“我们想把你踢下去。”
　　球说：“表，表，我讲，我讲。”
　　他们说：“数列数列。”
　　
　　于是球对他们小声说：“母测灌猹。”
　　然后就在地面上写了一长排数字。
　　他们看着，眼里闪着金光。
　　“哦！”他们说。
　　
　　“滚！”他们说。
　　
　　“你知道球为什么滚走了吗？”父亲问。
　　我当然知道。人又不是计算器，数学家也讨厌计算，他们是公式狂人。
　　
　　球滚走以后，他们三个就闷闷不乐地回家了。
　　但是现在我们都知道的是，有一个人看懂了。他走的时候回头看了一眼山上的数字，猛然发现那些数字的阵列从远处看去就是一个高耸接天的巨大公式。另两个人没有看见，因为他们都是近视。
　　几年后，有两个数学家郁郁而终。
　　从前的新闻是，今天我们镇有两个婴儿，一头牛，一头公猪崽出生，三个数学家以及十七只蟑螂死去。
　　
　　但其实没有，不然就不会有这本伟大的《数列》。
　　“或许活着。”父亲喃喃低语，手有些颤抖。
　　我抬起头，仿佛看见窗外一个大球正在滚来。
　　
　　《数列》上说：不动点法（或特征根法）是不可思议的，是一座“友谊”桥梁介于人类与神迹之间；数学归纳（或目测观察）是不可接近的，是一把“坟墓”钥匙破坏自然科学的金锁。 　　

1985

　　故事还可以继续讲下去。
　　1985年，人人都对上一年的高考的最后一题心有余悸。报纸上连续三个月报道了同样一题，并且，当年仅有的几个大出版社停下了所有的工作，开始印刷一本人们从未见过的叫《数列》的书。
　　
　　“1月20日电　在政府的英明领导下，截至1月19日全国已印刷《数列》约八亿七千五百万本，其中精装版七千六百万本。《数列》（俗称‘蓝宝书’）已成为每位公民的必读书目，将会为国家社会经济文化建设添上浓墨重彩的一笔。”
　　
　　传说在我家乡南面的一个小山村中，曾经走失过一位乡村数学教师。村里的老人谈到这个人的时候都只是微微一笑。但是难得的是，我的一个叔父曾在他的葬礼时，趁所有人都躲在门外哭泣，他掀开棺材盖板，将这件事告诉了我。然后，又悄无声息地爬回去，躺好，恋恋不舍地再次死去。我像帮婴儿盖被子一样轻轻合上厚重的棺材板，像老鼠一样蹦跳出门，流着泪混进嚎啕的人群中。
　　
　　《数列》的出版在推动社会进步的同时，也不可避免地带来了一些问题。例如许多人在拿到书的那一刻，就陷入了对那个卸载山上近乎神迹的公式的不懈证明中。但很快就有专家出来辟谣，说这个公式是不可能被严格证明的，其难度就如同一个常人妄图完全理解相对论或者一个天才企图发明永动机一样。在媒体报纸广播电视的大肆宣传下，轰轰烈烈的愚蠢的人民证明运动被打压下去了。但是可惜的是，在交通闭塞信息不通的山区，我们故事的主角乡村教师老兰偶然得到了一本数列，然而并没有任何人告诉他这是一本只能远望的书。
　　
　　老兰所教的小学有十几名学生，一个班，集合了附近几个村子里能吃饱饭的家庭的未成年人。学校有一个校长，但由于没有东西吃被饿跑了，老兰现在教所有的课。由于老兰是数学老师，孩子们一天有六节体育课以及一节数学课。
　　
　　如果恰好有一天所有的孩子们都逃了课，老兰就有一天来研究他的新书。他计划将这本书教给孩子们，但他在备课的时候遇到了一个难题，就是我们熟知的没有推导过程的不动点法公式。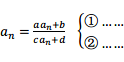

　　
　　在舆论的疯狂宣传下，几乎每一个人都明白了公式的用法。但专家的话也使得人们不希望再深究。就好像你拉出来一坨屎，但没有人希望通过屎的研究来了解你中午吃了什么，人们只要知道它是屎并且避开就够了。但老兰却不幸成为了研究屎者。
　　
　　1985年春，由于春节与孩子们对课堂的厌恶，老兰待在空旷的学校里一个月，以他能抓住的任何含蛋白质的生物为食。他念念不忘那个不可能被证明的公式，在学校的唯一一间房的每个墙面、天花板、烟囱、铁锅、红薯，甚至是跳来跳去的老鼠上写满了五颜六色的推导用数字符号。以至于当唯一散步经过学校的於七看来这仿佛就是加州的街头，充满了嘻哈、摇滚及朋克元素。
　　
　　有一天，老兰在睡觉的时候，有一只老鼠钻进了他的嘴里。
　　（那天夜里我曾与死去的叔父争论此事。他说老鼠的时候我感到莫大的怀疑，我甚至看是怀疑整个传说的真实性。我说叔父，您死糊涂了，怎么可能老鼠钻得进人的脑子呢？他说放屁，我比你早死五十年，我喝过的孟婆汤比你流过的血还多。我说叔父，说不定是您喝孟婆汤喝傻了，劣质的东西可能无法消除记忆只能打乱记忆。他惨白的脸努力变得通红，但是他失败了。他像一个死了二十年的人一样叹口气，说，不可能的，不可能的。不是老鼠就是大象，不是老鼠就是大象。我看他真的死糊涂了，就只好在这里以我的正确理解将故事再讲一遍。
　　那天一直蛤蟆钻进了他的脑子里。于是老兰开始做梦。他果不其然梦见了那个球。几十年来它一直在不停地滚来滚去。老兰说：“停！”。没办法，老兰只好说：“Stop！”那个球停住了。从里面走出来一个带着光环的年轻人。
　　“上帝呀！”老兰说。
　　“欸。”上帝说
　　
　　“你想获得力…”上帝说。
　　“快。”老兰说。
　　“滚。”老兰说。
　　在诱惑面前，老兰最后还是坚守住了做人的底线。它挣扎着拒绝了近在咫尺的答案，疯狂地想以自己的努力解出题目，维护数学的尊严。
　　
　　于是上帝滚起来，滚进了老兰的嘴里。
　　于是老兰醒了，拎着於七回到教室。
　　
　　老兰面色呆滞，眼神空洞，他的嘴同那晚叔父的嘴一样，用并非来自人间的声音说出：
　　“我们今天上数列。”
　　
　　老兰用近乎闪电般的速度向於七灌输了关于不动点法的绝无仅有的完整知识，就好像撬开他的脑子向里面塞满黄油然后又把它关上不留痕迹。
　　
　　於七呆呆地看着（或许他根本就没看）老兰滑行出了门。当老兰滑过村庄的时候，所有人都跑出来放下所有的东西目送着他，就好像目送着一个真正的上帝一样。摇篮径直滑过村庄，滑向不远处的山崖。
　　我知道我们都和村民期待的一样希望看见老兰像一架喷气式飞机一样升上天空。
　　但不巧的是，老兰还是在悬崖边上迅速不见了。
　　不过令人欣喜的是，正在崖边找吃的的校长信誓旦旦地说，她没有听见落地的声音。
　　
　　《数列》上说：
　　我们不应该歧视任何一个字词，就如同我们不应该歧视任何一个数字一样，就如同我们不应该歧视任何一个字母一样，就如同我们不该歧视任何一个符号（神迹）一样。 　　

1986

　　“一切没有写‘解’的论证都是荒诞而又可笑的。”
　　　　　　　　　　　　　　　　　——《数列》

　　1986年，我们的故事到了最后一年了。或许我的故事有胡编乱造的成分，但你不能强求太多。
　　於七躺在床上什么也不想。自从1985年来，他感觉他的脑袋像铅球一样大。他觉得痛苦的是，当他向他身边的所有人问起他的脑袋的大小的时候，他们都认为他有毛病，他应该去学习而不是对着一个个无所事事的人问脑袋。于是他只好开始想。但无论他想什么事情包括语文英语五子棋黑色白猫梦中情人的看不清楚的连与没有温度的嘴，竖列公式就像一泡反刍的草从四面八方涌上来，于是他轻飘飘的脑子就会越来越重，直到变成一个真正的铅球。
　　
　　1986年，我们的村庄里有人说：“夜里老兰的鬼魂在田里游荡。”
　　有人说还有我很多人的。
　　还有人说他们在打斗地主，他看见一对王炸。
　　
　　1986年，於七神奇地发现，事实上睡觉是一件无关紧要的事情，它是荒诞的，就像人们手淫或做爱一样毫无魔力可言。
　　于是於七总是在夜里出去游荡。那是一种真正的游荡，因为於七如果在想什么的话，他的脑子就会重到让他动不了。
　　我曾向每一个人求证过夜晚的田野是什么样子。我的父亲说充满鱼和青蛙，我的母亲说有可怕的蛇，我的外祖父说到处都是草和禾苗，我的外祖母说她没去过不知道。我只见过深夜的城市，空调的水从四面八方滴到我的头上肩膀上。
　　於七常常带一副扑克牌，然后分成三排围一个圈留三张，树下的风就会自动把三张牌吹向一边然后慢慢一张一张或几张几张把牌吹响中间。於七说他享受，他可以看一晚上，因为偶然性是他所需要也是必要的。只有完全的随机才能让他的脑袋安静下来，和他一起度过一个美好的夜晚。
　　
　　早在1985年，当最后一本《数列》被印刷出来以后，所有的印刷厂就如同一排土炮一样一齐哑火，那一天报纸上出现了最后一篇关于《数列》的报道：
　　“截至今日，《数列》的印刷已光荣完成使命。据可靠数据，全国十八岁以上成年公民已人手一本。”
　　但这样一篇报道没有引起任何人的注意，它夹在两个大块广告的中间。《数列》这本书早已出现在各家各户的桌下碗上厕所里，成为了又一件曾经辉煌的废物。
　　
　　原则上，《数列》这本书於七是不应该有的，他应该准备高考而不是做大人做的事情。但由于村里对老兰的消失心有余悸，没有人来管理老兰这最后的遗物。
　　於七在老兰拎着他时曾想，要是老兰腋下的这本书变成枕头该多好。但后来当他把书搬回家的时候书在他的手中越变越软，最后他把这本软的像枕头一样的书扔在床上。躺在《数列》上面让他与他的脑袋觉得舒服。并且他决定不再许愿。一是他一想头就重，二是他想把东西留给高考。
　　
　　高考那一天，看见於七的人分成了两排。一派说他们看见於七像老兰一样在村庄的地面上滑行，一派说他们根本就没看见於七。
　　
　　当於七看到数学的最后一题的时候，他知道这个故事本身就是荒诞的。就像所有人都预料到的一样，题目说，请推导出著名的数列公式。
　　于是於七的脑袋就开始变得比铅球更沉，甚至比你想到的东西都要沉。在这里有两种相似的解释，一是那个东西是如此沉重以至于他只能把它放在桌子上然后睡死过去；二是那个东西超乎想象的沉重以至于它的质量使时空扭曲使於七回到了过去。
　　所以我们可以说，19??年，於七看见了那个球。
　　球说：“还记得吗？”
　　於七：“有点忘了。”
　　球说：“现在的脑子质量越来越差。”
　　於七：“是的，因为社会进步。”
　　球与於七沉默了很久，最后球把於七的脑袋拔下来蹦上去，于是於七有了一个球脑袋。
　　“感觉好多了。”
　　因为球是德国制造。
　　
　　但是事情没那么简单。
　　“你骗了我。”於七想。他发现球有一些东西瞒着他。
　　“什么？”
　　“不，不对。”於七想，“你在欺骗我。”
　　“什么？我和你曾经那么…”
　　“不，你已经不是原来。”於七想，“我现在讨厌你。”
　　“没想到你是一个这么喜欢嫉妒的人。”
　　“我无法容忍你这样。你这是在背叛我。”
　　“我没有，我只是…”
　　“别再说了，我不想听你说话。”
　　“很多年前，我只是对他…”
　　“够了！”於七想象他吼出来，“滚。”
　　但这次球并没有滚起来，它又一次打开了於七的脑子，塞了一坨东西进去，关上，噗嗤一声重新扔到於七脖子上。
　　“好吧。”於七说，“我还是原谅你。”
　　
　　于是於七回到了现实，他的愿望帮助他获得了新生。
　　“他马上就要成为传奇了。”父亲说，“只是马上。”
　　於七抽出两支笔，左手一只右手一只，开始像打字机一样在卷子上面工作。如果有监考老师在旁边看的话，一定会为他优美的姿势叹服。於七在写的时候事实上没有感觉到那么多。被塞进他脑子的两坨东西正在一点一点流出。一遍就是我们熟知的不动点法，另一边就是只有在老一辈的传说里才有的目测观察法。而他则在想象中的安静的树下看风斗地主。他感到无比舒服就像周围的脏东西正在一点一点被清理一样。
　　
　　最后呢？我问父亲，他一副要睡着的样子。
　　他最后还是没写完，同我们每个人经历过的一样，左右开弓无疑拖慢了他的速度。有时右手还要停下来等一等左手。当老师把卷子收上去的时候，他的手依然还在桌子上抽动。最后，考古学家们根据桌上的印记与残缺的试卷，复原了於七的手稿。
　　而另一半目测观察法则神秘地完全遗失了，最可信的说法是它从来没有出现过。
　　
　　有个结尾。1986年，高考过后，人们经常在牌桌上看见於七斗地主 　　

外传

　　写这个外传的目的是希望你们不要搞错了，这是数学小说而不是语文小说。并且，我们也应该了解一下真实的1984。

　　有一天，我在奥数老师的柜子里乱翻。奥数老师在与父亲扯皮学费应该给多少的时候，我阅读到了下面的东西：

　　小学奥林匹克数学教程　　XXX主编　　1984年第2版
　　第七章　　　模与XX（忘了）
　　① 一个数模9等于它各位数字之和模9
　　② 整数运算： a×b=c,若a≡m (mod9), b≡n (mod9),则c≡mn (mod9)

　　（笔记）① + ② 可被用于验算

　　如果你还想看下去，那么我解释一下：
　　一个数模9是指它除以9的余数，a≡b (mod9)是指a与b除以9余数相等
　　例：23÷9=2⋯5，所以23模9等于5，23≡14≡5(mod9)
　　所以说人话：
　　例：156除以9的余数等于1+5+6除以9的余数等于3
　　证明：12 × 13 = 156，根据余数定理，因为12除以9余数为3，13除以9余数为4，12×13除以9的余数 = 3×4除以9的余数 = 3

　　所以这个东西的唯一用处就是检验你算对了没有。
　　最后啰嗦一句，实际上老师坚持免我的学费，爸不同意，最后各退一步收了3500。